Did you solve it? Are you cut out for these puzzling slices?

Earlier today, I set you these three geometrical puzzles. Here they are again with solutions.

1. Bonnie Tiler

Below left is a square grid with three of its corner cells missing. Below right is a tile made of three cells in a line.

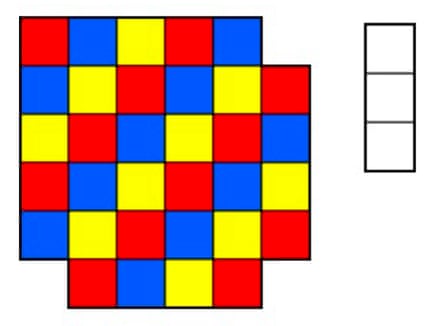
Given that there are 33 cells in the grid, can you cover it with 11 of these tiles? If not, why not?

Solution No, you cant. Every position of the tile covers a blue, yellow and red cell. If a covering existed, the grid would have to have 11 cells of each colour. But there are 12 red cells and 10 yellow ones.

2. Assembly needed

The left-hand shape below can be cut into four identical pieces, cutting only along the black lines, which can be fitted back together to make a square, as shown in the right-hand shape.

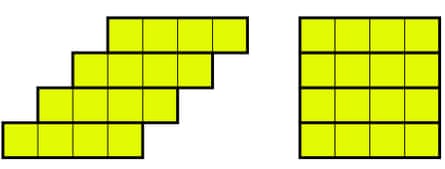
Can you find a different way to cut the left-hand shape into four identical pieces that can be rearranged to make a square? (The pieces may be rotated or reflected.)

Solution

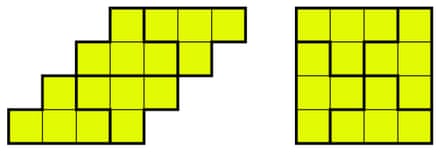
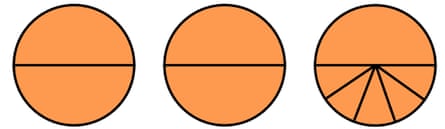
3. Pizza party

Below is one way to divide three pizzas among five people. Three people get a 3/5 slice, and two get a 2/5 and a 1/5 slice. Another way would be to divide each pizza into five equal slices, with each person getting three.

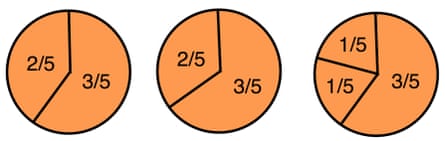
What’s the smallest number of pieces so that each person gets exactly the same numbers and sizes of pieces?

Solution Ten pieces. Each gets a half and a tenth.

Thanks to Ian Stewart for today’s puzzles. His new book Reaching for the Extreme is out on February 12 and can be pre-ordered at the Guardian Bookshop.